by Kazeem Olalekan CEO Iforg Limited
In the early days of Iforg Limited, I have always blogged about issues that excited my interest. On the 25th of March 2007 (over 8 years ago now! How time flies), I posted one of those blogs which I entitled: “The Power of Observation – the pill counter example”. My aim was to illustrate in a graphic way, what Iforg Limited was and is about. I have decided to re-visit that blog because it is fundamental to what I am trying to achieve with Iforg. I am re-posting it below. Enjoy!
as posted on 25th March 2007 on the old Iforg Limited website:
The Power of Obeservation – the pill counter example
by Kazeem Olalekan
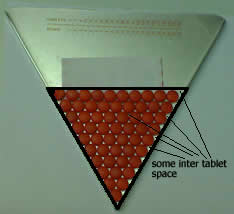
If you have ever worked in a pharmacy, you will recognise the ubiquitous triangular pill counter (figure 1). Ever wondered how the row of numbers were derived?
Figure 1
The row of numbers looks something like this (figure 2):
Figure 2
So if you have 7 rows of tablets, the number of tablets you would have counted is 28 and so on. The question of how these numbers were derived exercised my curiosity recently. I wanted to develop a mathematical model for working out these numbers. The process I went through highlighted some profound issues relating to the power of observation.
An approach to solving the problem [Model 1]:
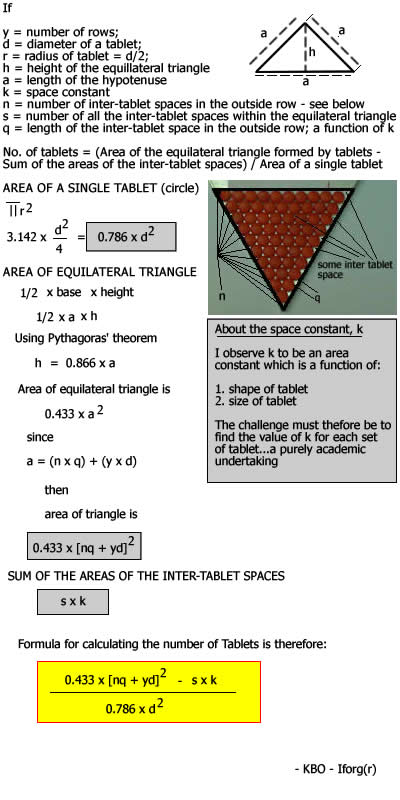
What seemed obvious to me initially, was that the number of tablets in the row of numbers will only work when the tablets being counted are round, forming a triangle of tablet which is equilateral (having all sides of equal length) – Figure 1. The model should therefore look something like this:
No. of tablets = (Area of the equilateral triangle formed by tablets – Sum of the areas of the inter-tablet spaces) / Area of a single tablet
As in figure 3 below:
Figure 3
Simple? Not really (see box 1 below)
Box 1
This way of solving a problem makes the idiomatic expression about a sledgehammer and a nut very apt.
Another approach – Observation [Model 2]!
Observing the way the tablets are arranged in the triangle provide a better insight. Provided the tablets are round and the triangle: equilateral, a pattern seem to emerge:
1st row = 1 tablet
2nd row = 2 tablets
3rd row = 3 tablets
4th row = 4 tablets…etc
No. of tablets = sum of the tablets in each row
Therefore, if there are 5 rows, then
No. of tablets = 1 + 2 + 3 + 4 + 5 = 15
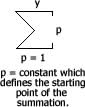
for y = number of rows;
No. of tablets = 1 + 2 + 3 + 4 +….+ y
This is a classic triangle sequence (1,2), which is well known to mathematicians and can be represented as (figure 4):
Figure 4
This approach to solving a problem reminded me of the article by John C. Harrison – The Power of Observation in which he described an encounter with Frijof Capra, the author of The Tao of Physics (Flamingo)
We arrived at those advanced concepts (about the picture of the universe) through careful scientific reasoning. The Chinese got there by simply observing.
Whilst the two models described above will eventually provide identical answers to the problem, Model 2 is clearly a more desirable model, especially if like me, you are time poor. Observation may prove to be the key for improving efficiency and productivity. Harrison wrote:
….all personal changes begins with observation….the challenge, then, is to learn to observe objectively
Objective observation defines Iforg’s approach to all our projects and we expect to make efficiency and productivity savings as a result.
In November of that year, I recorded a podcast with Kate Penhaligon based on this post.
[sc_embed_player fileurl=”http://www.iforg.net/podcast/0UzPD10-Nov-07.mp3″]
